The world today
Maybe you have heard here and there about some technological wonders based on artificial neural networks -- about intelligent robots, smart weapons or even stock trading advisory systems? What's going on? Are we really living at the turning point of history where machines are taking over and mankind will be doomed? To be honest, it is not completely impossible, but artificial neural networks in their current state of evolution are hardly the right target for accusations of that kind. The most complex neural networks of our time are not working in the dark corners of high-tech labs. No, they are in our heads.
Start thinking!
How much do we know about the inner mechanisms of our brain? How often do we think about how exactly we think about the things we think about? The fact that this sentence looks a bit weird should be considered alarming as it shows the lack of discussions on the topic. Think about it!
Biology
Human brain is an extremely complex structure. Its workings can be discussed on a huge number of different levels -- starting from the low end of atoms and molecules and going up to the social interactions of global scale. All these levels are remarkably interesting, but as our current concern is artificial neural networks, we will go to the cellular level.The main component of our biological neural net is a cell called neuron. Many different types of neurons are present in brain, but their general structure is mostly the same:
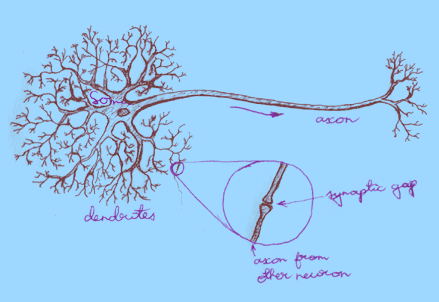
On the drawing you can see the main parts of a neural cell:
The main principle of neuron's work is already visible from the description of its structure -- neuron collects signals, processes them and feeds into other neurons. In reality, however, everything is very complex. First of all, signals are far from simplicity. They are passed via electrochemical processes based on different ions (mainly sodium (Na), potassium (K) and chloride (Cl)). Even worse, the information is coded not into the amplitude of signals, but instead into frequency of these electrochemical pulsations (although that doesn't automatically mean we could just forget about the amplitude). Secondly, although the scales are microscopic, the numbers are macroscopic. Each neuron has up to 10,000 input connections via dendrites, all passing signals into the soma. And the number of such neurons in a brain is estimated to be somewhere between 10 and 100 billion (thats 10,000,000,000 and 100,000,000,000)! Finally, all this unimaginably huge system is in constant change -- new connections are being formed, some cells stop functioning due to aging, etc.
- Dendrites collect incoming signals. They have a lot of branches and their surface is quite irregular. Dendrites got their name because of a tree-like structure.
- Soma is the body of the neural cell. It processes incoming signals (and, of course, performs all the activities necessary for a cell to survive).
- Axon transmits signals to the dendrites of other neurons. Axon has less branches, smoother surface and greater length than dendrites.
- Synapses are connections between neurons. They are actually tiny gaps that allow signals to jump from an axon to a dendrite.
Technology
- Todays technology is nowhere near the complexity described
in previous paragraph, neither in numbers nor in principles. Although artificial
neural networks DO have some resemblance to their biological counterparts,
they are still tiny and simple structures. Their simplicity, however, does
NOT mean they are fully understood and easily described by mathematical
tools.
Artificial neuron
- There are a great many different models of neurons and
neural networks, lots of them being successfully used in various applications.
Still, most of them have a lot in common and differ only in details. The
most widespread structure of an artificial neuron is:
- On the left there are inputs x1, x2, ..., xn.
- Each input goes through a connection, wich has a certain weight w, and is multiplied by that weight: x * w.
- All these multiplied values are then added together:
- This sum u is then adjusted with threshold t:
- And finally a so called "activation function" F() is applied to the adjusted sum, giving us the output of neuron:
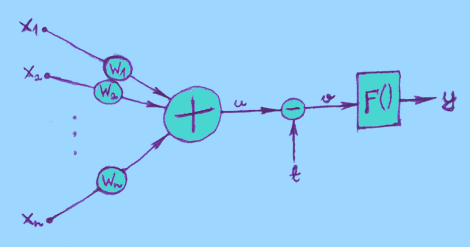
If it looks a bit messy and scary first, then don't worry,
actually it is very simple.
- u = x1*w1 + x2*w2
+ ... + xn*wn
- v = u - t
- y = F(v)
There are three basic types of activation function F():
- 1. Threshold function (not to confuse with threshold parameter
t):
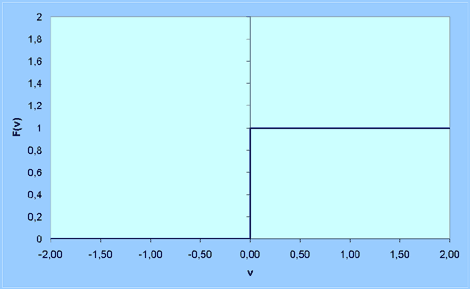
F(v) = 0, if v < 0
F(v) = 1, if v = 0 or v > 0
2. Piecewise-Linear function:
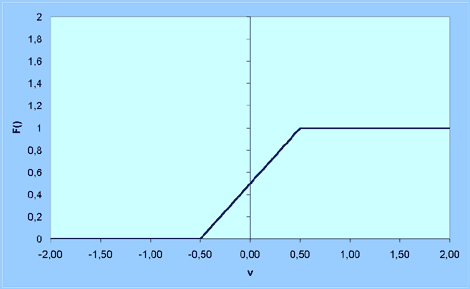
F(v) = 0, if v < -0.5 or v = -0.5
F(v) = v + 0.5, if -0.5 < v < 0.5
F(v) = 1, if v = 0.5 or v > 0.5
This is just an example, it may have other values as well.
3. Sigmoid function:
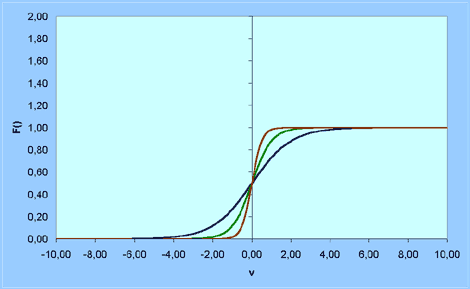
F(v) = 1 / (1 + exp(-av)), where a is the slope parameter.
Three examples with different a are given on a chart.
The sigmoid function above is known as "logistic function",
but there are other forms of sigmoid function, too. For example:
F(v) = tanh(v / 2) = (1 - exp(-v))
/ (1 + exp(-v))
Sigmoid functions are the most common activation functions used in artificial neural networks.
Artificial neural network
- As already mentioned before, there is a plethora of different
network models, and the level of similarity is considerably lower than
it was in artificial neurons. We can compare the neuron with a building
block -- by using standard blocks it is possible to build a great number
of houses in different styles. Start customizing your blocks and the possibilities
jump to infinity.
The most common class of ANNs is multilayer feedforward networks:
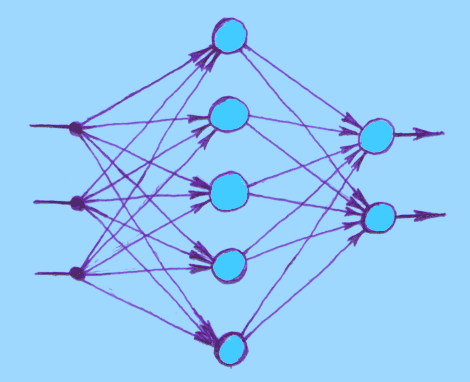
It has a layered structure. Input nodes, whose only
purpose is to distribute the input values into network, form an input layer
(on the left on picture). All other nodes are artificial neurons, which
also form layers: the output layer (on the right), and between input and
output layers is one or more "hidden" layers. "Feedforward" implies that
signals move only towards outputs -- no feedback loops are present. Network
on the picture is "fully connected" in the sense that every neuron in each
layer is connected to every other node in its neighbouring layers. If some
connections were missing, it would be a "partially connected" network.
Training a network
- If you have carefully followed the story so far, you
probably already have some ideas about how ANN will work: it is given a
bunch of input values, it processes them and gives back some output values.
Clean and simple :) Except one problem -- we would like the ANN to have
a REASONABLE reaction to given inputs, not just any random reaction! That's
were training comes in.
- Input values are fed into network.
- Network's reaction (output values) is read out and compared to the desired reaction.
- Error values are calculated out of the difference between desired and actual outputs using some error function.
- The weights of connections owned by output layer are adjusted according to the error values.
- Error values are then BACKpropagated to the hidden layer next to output layer, and its weights are adjusted.
- Backpropagation and weight adjustment is repeated until input layer is reached.
- The whole procedure is repeated until error is acceptably small.
As there are different architectures of networks, there
are also appropriate training algorithms for each of them. From network's
point of view it would make more sense to call them learning algorithms,
especially because some of them do not require any teacher (unsupervised
learning). However, in case of multilayer feedforward networks a supervised
learning procedure is used most often, usually a "backpropagation" algorithm.
Its principle is:
The point of using ANNs is that although we train
them only with a few training patterns (which consist of input values and
desired output values for these inputs), the ANN can also correspond reasonably
to the inputs that are similar to the learned ones, but not exactly the
same. This is called "function approximation" and is quite useful in many
applications.
The details of training procedure usually contain heavy
math and are not easily grasped. Following is just a short overview about
HOW the backpropagation can be done. Answering the question "WHY it can
be done that way" would definitely be more reasonable and enlightening,
but I'm currently not up to the task of doing it, especially in a user
friendly way :) Anyway, if you get an intense feeling of repulsion when
looking at the following section, then feel free to skip it and scroll
down to the next paragraph.
- First of all, the calculation of output values is done
using the neuron model descibed above (input values are set into the input
layer; then all neurons in first hidden layer are updated according to
the neuron model; then neurons in second hidden layer; ... ; until output
layer is reached).
Now we have output values for this given set of input values, but most likely they are not what we want them to be. So we can calculate error value for each neuron in the output layer.
- error_value = desired_output - actual_output
- error_signal = error_value * F ' (v)
where v is the adjusted sum in neuron (see the neuron model above) and F ' (v) is the derivative of activation function F() in point v.
- w1 = w1 + learning_rate * error_signal * x1
w2 = w2 + learning_rate * error_signal * x2
...
- where x1, x2, ... are inputs into this neuron from neurons
located in previous layer (once again, see the neuron model above) and
learning_rate is a parameter affecting the speed of learning (it should
be noted that it is also a "forgetting speed" in some sense -- if learning_rate
is very high, then network quickly learns new training patterns, but on
the cost of forgetting others; plus additional danger that ANN becomes
so instable it can't learn any single pattern at all, like a hyperactive
child.).
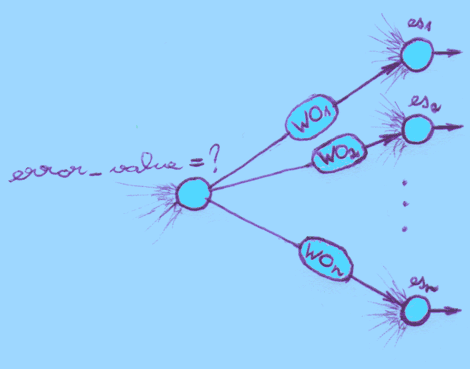
- error_value = wo1* es1
+ wo2*es2 + ... + won*esn
where "wo" is the weight of a connection between current neuron and a neuron in following layer (see the picture above), and "es" is the error_signal of that other neuron.
It is quite likely that you have at least one question after reading previous algorithm: what exactly is the derivative of F(v) and why is it used anyway? It should be clear that F ' (v) is not the same for all activation functions F(v). One of the most common activation functions is F(v) = 1 / (1 + exp(-av)) and it's derivative is mostly given in a form F ' (v) = a * y * (1 - y), where y = F(v) (y is the output of the neuron, see neuron model above). It may be somewhat surprising first, but if you take a few minutes and try it on a paper then it makes more sense. First you get a big messy derivative, but some replacements should reduce it down to given short form which is much easier to use than the big messy one. Why is derivative needed, anyway? Because backpropagation is a gradient descent algorithm, meaning it tries to move the system towards the deepest descent on error surface for getting the fastest reduction of error. But finding the deepest descent of a surface is, naturally, done by using gradient, which in turn is found by using derivatives. As simple as that :) Feel free to search for additional information from Internet or books.
What can be done with ANNs?
- As we have now seen, artificial neural networks are very
far from the complexity of their biological counterparts. There is also
an additional problem -- in brain all neurons are working all the time
(in parallel), but our computers work in sequential fashion, meaning they
have to update artificial neurons one by one which is an awfully time-consuming
process. Special hardware can be built for ANNs, but often it would be
too expensive. So a question rises: do we need ANNs at all? Where?
The answer is: although ANNs probably are NOT the hoped breakthrough in Artificial Life research, they do have turned out to be very useful in many fields of technology. ANNs have been successfully used in various signal processing applications from sonar and radar classificators to word recognizers. They have a lot of use in industry: process control, quality prediction and inspection systems, process and machine diagnosis, etc. In robotics ANNs are used for vision systems and for controlling the robot's movements. Business applications include price prediction programs for stocks and currencies. ANNs can also be used in computer games and animations for various purposes like controlling the character movement or doing some other necessary decisions.
Summary
- This was just a short introduction to the field of ANNs.
Only one neuron model, one network architecture and one training algorithm
were described and even this was done without much details. Currently I do
NOT have any plans to write more essays on standard ANNs, so this page is
unlikely to be filled with any further information. However, there is a
great variety of materials available on Internet and in books, for beginners
and for professionals. If you DO have interest in the topic, please take some
time and look for more information. A few links are provided in Links section,
accessible from the front page. But before clicking away towards the shining
mountains of wisdom, please check out some educational software based on the
same models described in this essay: see the Software section on the front page.